16  Module 4.2: Population Structure

Population structure in crop breeding refers to the presence of clusters or subpopulations that are genetically distinct from each other. The subpopulations may reflect geography, breeding history, natural selection, gene pools, or other differentiating factors. The subgroups are identified by differences in allele frequencies.

16.1 Why is it important?

  • Allows us to detect subpopulations and understand genetic diversity

  • Can be used to control bias in GWAS or other genomic prediction models (by including structure information as covariates), as not accounting for structure may lead to spurious associations (false-positives)

  • Acknowledging structure can help guide breeding programs

16.2 Common methods

  • STRUCTURE / ADMIXTURE: Uses Bayesian clustering or Maximum Likelihood (ML) estimation to assign individuals into subpopulations, including admixture proportions for each individual.

  • Principal Component Analysis (PCA): Used to reduce dimentionality of large data sets, and to visualize overall diversity and major genetic groupings.

  • Spatial Principal Component Analysis (sPCA): Incorporates spatial information (geographic location) intro traditional PCA, meaning it seeks to maximize spatial autocorrelation along with variation. It allows us to identify global and local trends.

  • Discriminant Analysis of Principal Components (DAPC): Used to assign individuals to groups, provide a visual assessment of between-population differentiation and the contribution of individual alleles to the population structure.

  • Sparse Non-negative Matrix Factorization (sNMF): Fast algorithm used to infer structure by estimating ancestry coefficients. Allows us to evaluate levels of admixture. More efficient than STRUCTURE for large data sets.

All methods are complementary to each other and using them in combination can help us fully understand structure in our data.

Want to explore structure quickly? PCA
Want to analyze spatial genetic variation? sPCA
Need to classify individuals into groups? DAPC
Need to estimate admixture proportions? sNMF

We will be using functions from our package to carry out and visualize most of these analyses.

16.3 PCA

PCA reduces our large genotype matrix into principal components which capture the variation in our data. We will use the PCAFromMatrix() function from our package. This function uses the PCA framework from the ade4 package. This function returns a list with three objects, the first one being a PCA, the second one being a data frame with the variance explained by each component, and the third one being a plot of the PCA results (1st and 2nd PCs).

PCAFromMatrix(geno, subgroups = NULL): returns a pca object from genotype matrix

  • geno: our genotype matrix

  • subgroups: defaults to NULL, can be replaced with a vector of our factor information

# Importing filtered genotypic data
matrix <- read.table("data/FilteredBarley.txt", sep = "\t", header = TRUE, row.names = 1, check.names = FALSE)
# SNP matrix has to have individuals in rows and markers as columns for the posterior functions
matrix <- t(matrix)

# Importing metadata
metadata <- read_excel("data/BarleyMetadata.xlsx")
# We will be guiding our analysis by the 'countryOfOriginCode' column from our metadata
# Defining our subgroups
popSet <- as.factor(metadata$countryOfOriginCode[metadata$Individual %in% rownames(matrix)])
# Running our pca using our genotype data and groups
pca <- PCAFromMatrix(matrix, popSet)

# Printing pca object
pca$pca
Duality diagramm
class: pca dudi
$call: dudi.pca(df = x.genInd, center = FALSE, scale = FALSE, scannf = FALSE, 
    nf = round(ncol(geno)/3, 0))

$nf: 487 axis-components saved
$rank: 487
eigen values: 288 231.5 102.3 71 37.18 ...
  vector length mode    content       
1 $cw    12141  numeric column weights
2 $lw    488    numeric row weights   
3 $eig   487    numeric eigen values  

  data.frame nrow  ncol  content             
1 $tab       488   12141 modified array      
2 $li        488   487   row coordinates     
3 $l1        488   487   row normed scores   
4 $co        12141 487   column coordinates  
5 $c1        12141 487   column normed scores
other elements: cent norm 
# Printing PC variation
head(pca$var)
  PC  Variance CumulativeVar
1  1 17.004415      17.00442
2  2 13.666554      30.67097
3  3  6.040506      36.71148
4  4  4.191208      40.90268
5  5  2.195083      43.09777
6  6  1.665563      44.76333
# Plotting pca results
pca$plot

16.4 sPCA

We will be using the sPCA() function from our package. This function uses the sPCA framework from the adegenet package. It returns a list with our sPCA object, a plot of the obtained eigenvalues, results and plots for the global test and results and plots for the local test. The obtained sPCA result can be plotted using the sPCAMapPlot() function.

sPCA(geno, subgroups = NULL, xy, eigenPlot = TRUE, tests = TRUE): returns sPCA from genotype data

  • geno: our genotype matrix

  • subgroups: defaults to NULL, can be replaced with a vector of our factor information

  • xy: a two column longitude - latitude vector or data frame

  • eigenPlot: defaults to TRUE, plots the resulting eigenvalues

  • tests: defaults to TRUE, carries out global and local tests

sPCAMapPlot(spca, geno, xy, axis = 1, pos = TRUE): plots our sPCA results on a map

  • spca: our spca object

  • geno: our genotype matrix

  • xy: a two column longitude - latitude vector or data frame

  • axis: defaults to 1 (our first axis), we can choose any other axis to plot

  • pos: defaults to TRUE to plot the positive values, can be set to FALSE to plot the negative values

# Running sPCA
spca <- sPCA(matrix, subgroups = popSet, xy = metadata[,c("LON","LAT")], eigenPlot = TRUE, tests = TRUE)

# Plotting our obtained eigenvalues
spca$eigenPlot

# Plotting global test results
spca$globalTest

# Plotting local test results
spca$localTest

# Plotting our results in a map
sPCAMapPlot(spca$spca, matrix, xy = metadata[,c("LON","LAT")], axis = 1, pos = TRUE)

16.5 DAPC

DAPC requires the user to define a range of subpopulation numbers for which to perform the analyses. To do this, we can calculate different k-statistics to guide our choice of this range. We will be using our kMeansStats() function, which allows us to choose between "BIC", "AIC" or "WCC" for our desired k-statistic. This function outputs a data frame with our k-statistic values, and a plot. We will then use our DAPC() function on our genotype data, which uses the DAPC framework from the adegenet package. This function outputs a list with the dapc object and a data frame with the explained variances. An additional plot can also be produced.

kMeansStats(geno, pca = NULL, maxK, stat): returns test statistic results for different K values

  • geno: our genotype matrix

  • pca: defaults to NULL, can be replaced by a pca object to skip over creating a new PCA

  • maxK: the maximum number of K subpopulations for which to calculate k-statistics

  • stat: type of k-statistic to calculate

DAPC(geno, krange, subgroups = NULL, pca = NULL, dapcPlot = FALSE): performs DAPC

  • geno: our genotype matrix

  • krange: a range of K values

  • subgroups: defaults to NULL, can be replaced with a vector of our factor information

  • pca: defaults to NULL, can be replaced by a pca object to skip over creating a new PCA

  • dapcPlot: defaults to FALSE, if TRUE, an output plot is produced

# Calculating our K statistics
BICDAPC <- kMeansStats(matrix, pca$pca, 10, "BIC")

# Plotting K statistic
BICDAPC$statPlot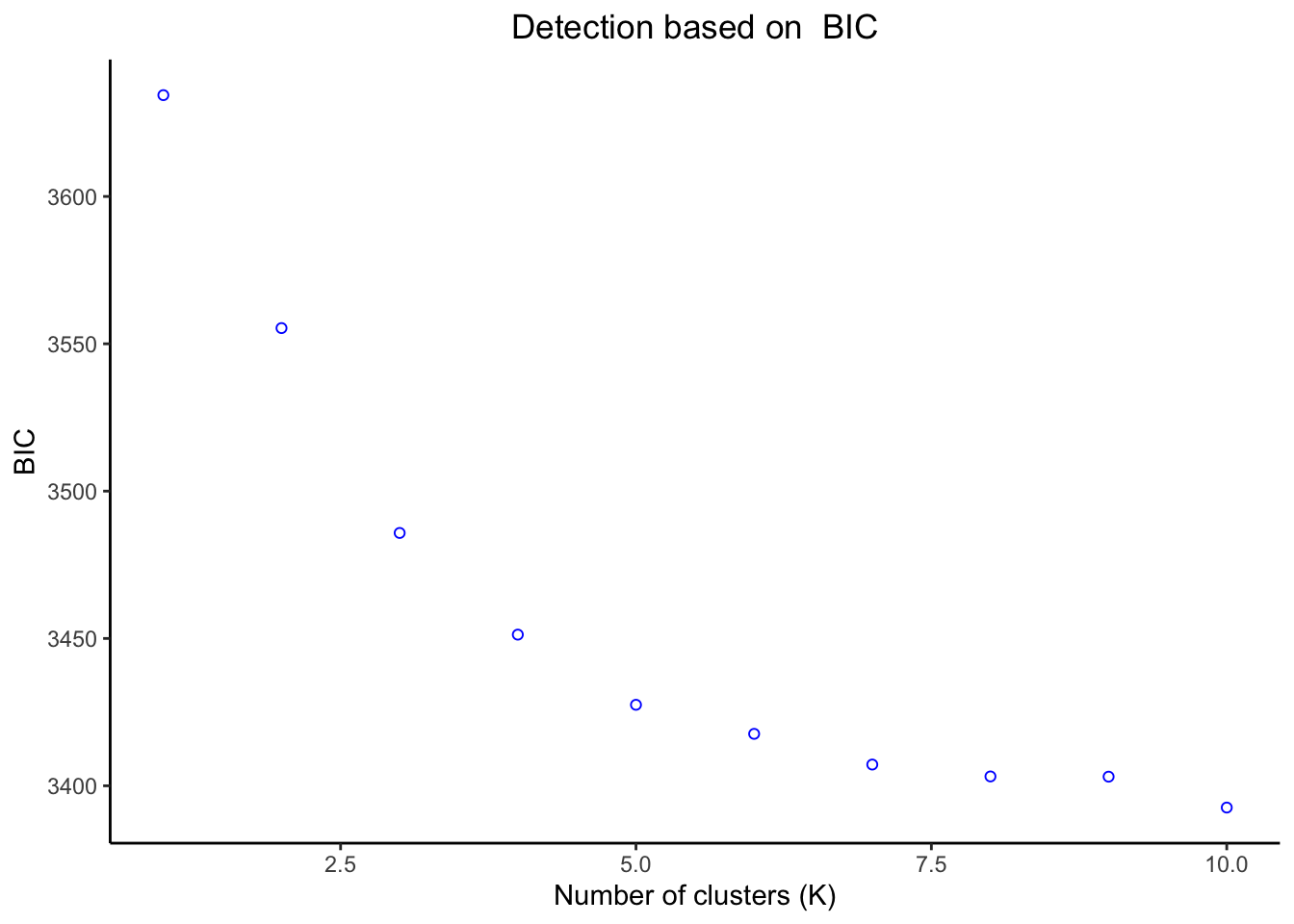

# Running DAPC
DAPC <- DAPC(matrix, krange = 3:6, pca = pca$pca, subgroups = popSet, dapcPlot = TRUE)

# Plotting DAPC results
DAPC$dapcPlot

Our resulting DAPC outputs group assignments for each individual, which can be visualized through a composition plot.

DAPCCompoPlot(DAPC, geno, krange, subgroups = NULL): returns a composition plot of DAPC results

  • DAPC: a dapc object

  • geno: our genotype matrix

  • krange: a range of K values

  • subgroups: defaults to NULL, can be replaced with a vector of our factor information

DAPCCompoPlot(DAPC$dapc, matrix, krange = 3:6, subgroups = popSet)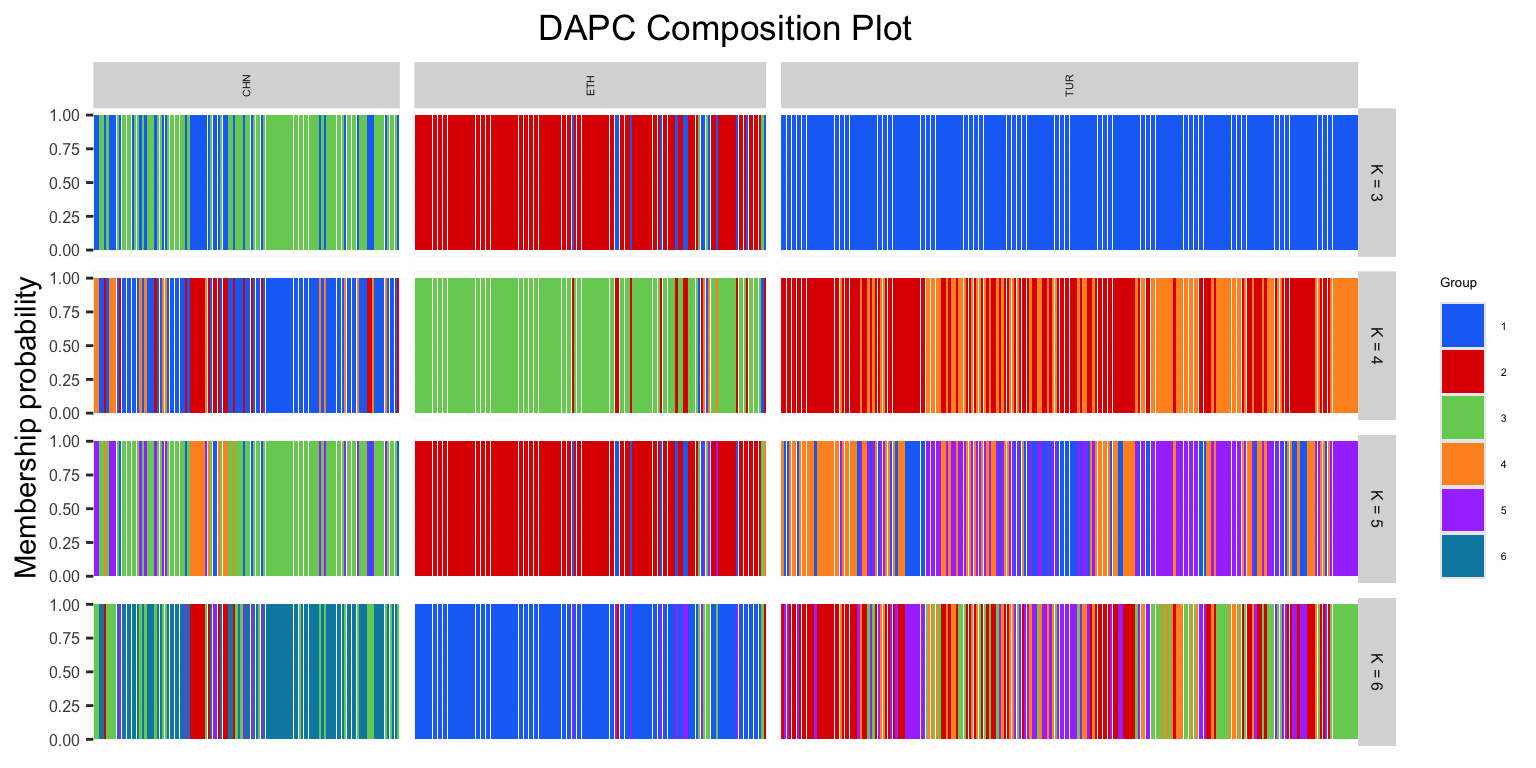

We can also produce a frequency plot from our DAPC. This helps us understand the relationship between the produced group assignments and prior group information we may have.

DAPCFreqPlot(DAPC, subgroups): produced a frequency plot of our DAPC results

  • DAPC: a dapc object

  • subgroups: a vector of our factor information

# For k = 3, which is our first object in our DAPC object
DAPCFreqPlot(DAPC$dapc[[1]], subgroups = popSet)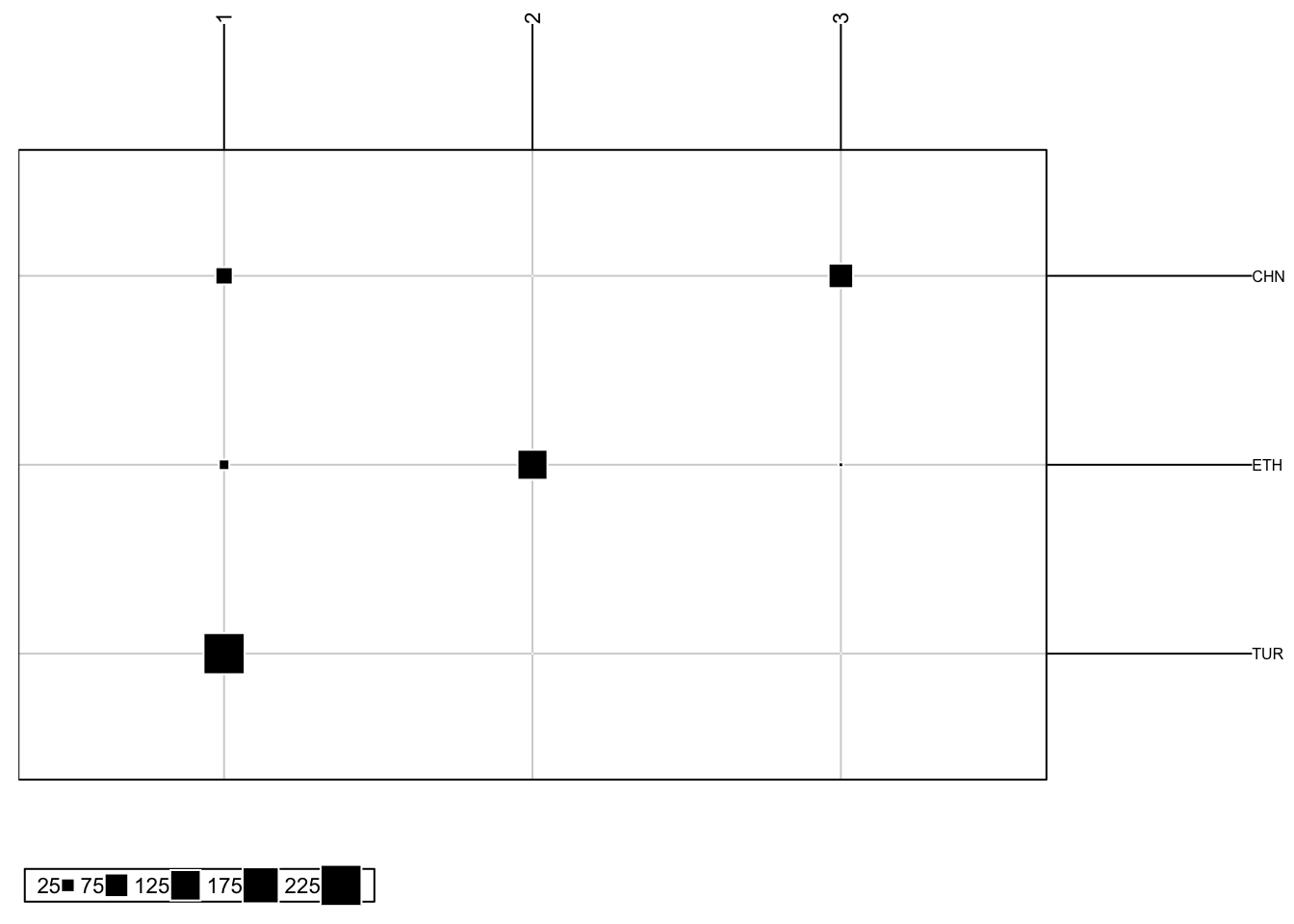

16.6 sNMF

sNMF is used to estimate admixture proportions: how much of an individual’s genome comes from different ancestral populations. This means that individuals are not just assigned to a population, instead membership probabilities (admixture coefficients) are calculated. We will be using functions from our package to carry out these analyses. The framework they use comes from the LEA package. Prior to estimating ancestry coefficients, this package requires us to create a geno type object, which we will create using the write.geno.mod() function. We can then run our main function using sNMFFunction(), which outputs a list with our snmf object, a matrix with the produced ancestry coefficients, and a data frame with cross-entropy values. The latter can guide our choice of best K value.

write.geno.mod(geno, output.file): creates geno type object from genotype matrix

  • geno: our genotype matrix

  • output.file: file path where to save our object

sNMFFunction(geno, file, maxK, subgroups = NULL, cePlot = TRUE): outputs ancestry coefficients

  • geno: our genotype matrix

  • file: file path of geno object

  • maxK: the maximum number of K subpopulations

  • subgroups: defaults to NULL, can be replaced with a vector of our factor information

  • cePlot: defaults to TRUE, outputs a plot of cross-entropy values

# Creating 'geno' object needed to run sNMF
write.geno.mod(matrix, "output/sNMFgenoBarley.geno")

# Running sNMF
sNMF <- sNMFFunction(matrix, subgroups = popSet, "output/sNMFgenoBarley.geno", maxK = 6, cePlot = TRUE)

We can visualize our membership probability results using a composition plot.

sNMFCompoPlot(sNMFmatrix, geno, krange, subgroups = NULL): returns a composition plot of admixture results

  • sNMFmatrix: ancestry coefficient matrix

  • geno: our genotype matrix

  • krange: a range of K values

  • subgroups: defaults to NULL, can be replaced with a vector of our factor information

# Plotting composition plot
sNMFCompoPlot(sNMF$qmatrix, matrix, krange = 2:6, subgroups = popSet)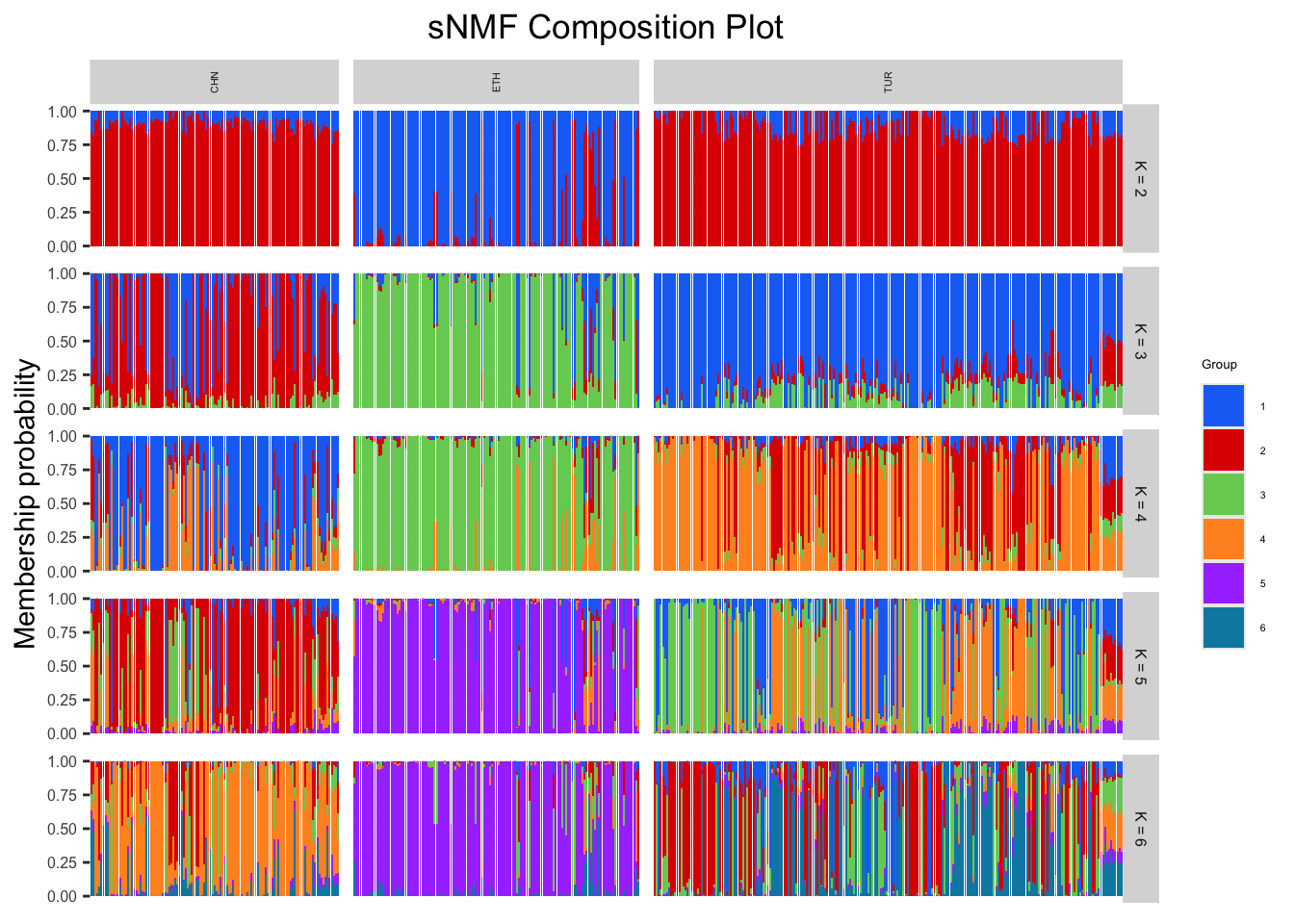

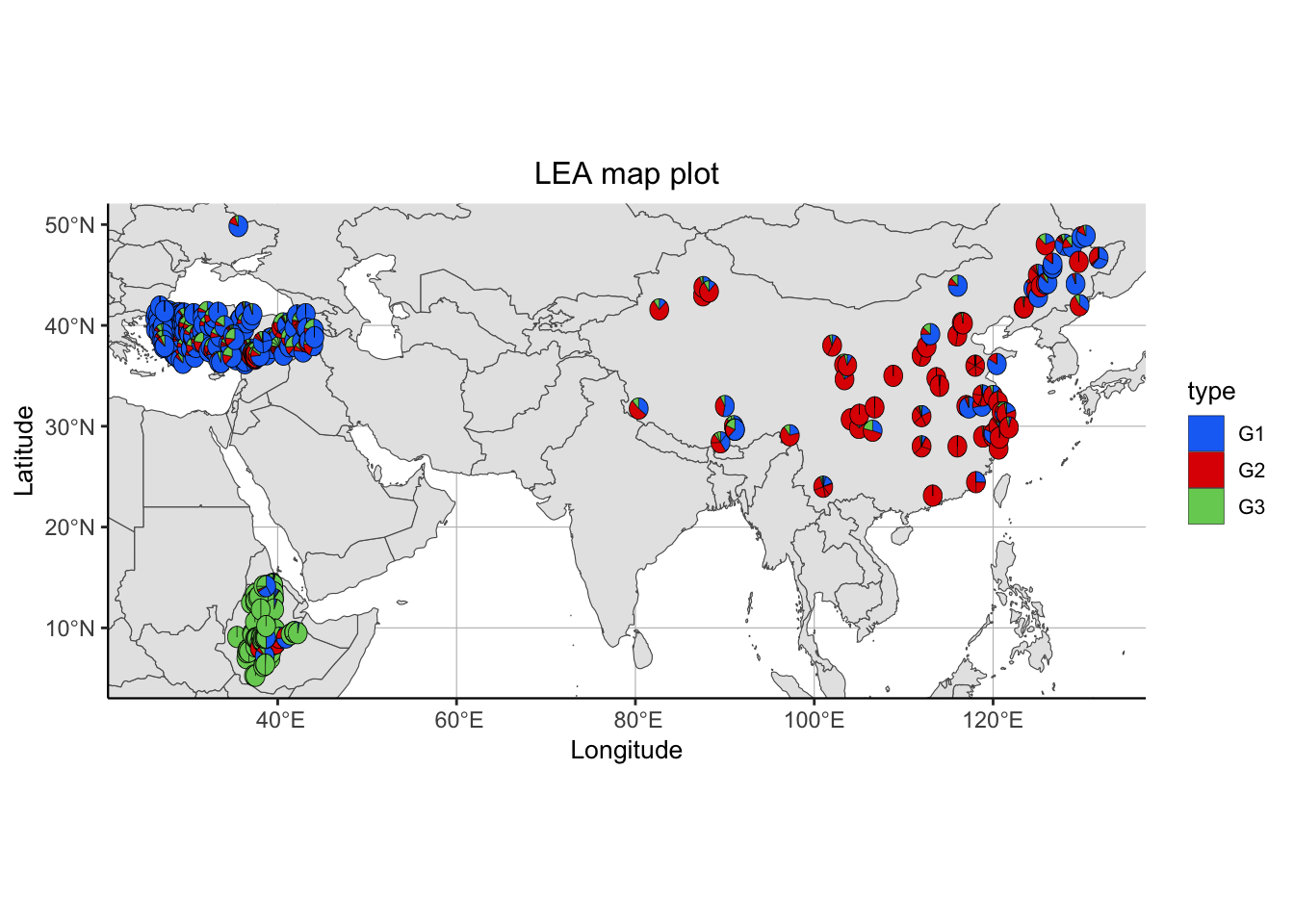
Finally, we can also visualize our sNMF results on a map by incorporating spatial information if available.

sNMFMapPlot(geno, sNMFObjectVar, xy, k, Xlim = NULL, Ylim = NULL): produces a map plot from ancestry coefficient results for a specific number of subgroups

  • geno: our genotype matrix

  • sNMFObjectVar: a snmf object

  • xy: a two column longitude - latitude vector or data frame

  • k: a number K of subpopulations

  • Xlim: defaults to NULL, can be replaced by a range of longitudes to zoom in the map

  • Ylim: defaults to NULL, can be replaced by a range of latitudes to zoom in the map

# Plotting results in map
sNMFMapPlot(matrix, sNMF$snmf, xy = metadata[,c("LON","LAT")], 3)